Общие понятия и определения. — IT1406: Информационная безопасность — Бизнес-информатика. Система остаточных классов - введение
Уравнение деления (), рассмотренное в предыдущей секции, имеет два входа (a и n ) и два выхода (q и r ). В модульной арифметике мы интересуемся только одним из выходов - остатком r . Мы не заботимся о частном q . Другими словами, когда мы делим a на n , мы интересуемся только тем, что значение остатка равно r . Это подразумевает, что мы можем представить изображение вышеупомянутого уравнения как бинарный оператор с двумя входами a и n и одним выходом r .
Операции по модулю
Вышеупомянутый бинарный оператор назван оператором по модулю и обозначается как mod . Второй вход (n ) назван модулем . Вывод r назван вычетом . Рисунок 2.9 показывает отношение деления по сравнению с оператором по модулю.
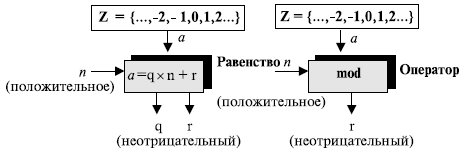
Рис. 2.9.
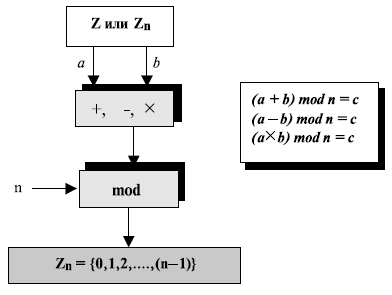
Рис. 2.13.
Фактически применяются два набора операторов: первый набор - один из бинарных операторов ; второй - операторы по модулю. Мы должны использовать круглые скобки, чтобы подчеркнуть порядок работ. Как показано на рис. 2.13 , входы (a и b ) могут быть членами Z или Z n .
Пример 2.16
Выполните следующие операторы (поступающие от Z n ):
а. Сложение 7 и 14 в Z 15
б. Вычитание 11 из 7 в Z 13
в. Умножение 11 на 7 в Z 20
Решение
(14+7) mod 15 -> (21) mod 15 = 6 (7–11) mod 13 -> (-4) mod 13 = 9 (7x11) mod 20 -> (77) mod 20 = 17
Пример 2.17
Выполните следующие операции (поступающие от Z n ):
a. Сложение 17 и 27 в Z 14
b. Вычитание 43 из 12 в Z 13
c. Умножение 123 на -10 в Z 19
Решение
Ниже показаны два шага для каждой операции:
(17 + 27) mod 14 -> (44) mod 14 = 2 (12 – 43) mod 13 -> (–31) mod 13 = 8 ((123) x (–10)) mod 19 -> (–1230) mod 19 = 5
Свойства
Мы уже упоминали, что два входа для трех бинарных операторов в сравнении по модулю могут использовать данные из Z или Z n . Следующие свойства позволяют нам сначала отображать два входа к Z n (если они прибывают от Z ) перед выполнением этих трех
В криптографии и криптоанализе часто бывает необходимо сложить две последовательности чисел или же вычесть одну из другой. Такое сложение и вычитание производится, как правило, не с помощью обычных арифметических действий, а с помощью операций, называемых модульной арифметикой. В модульной арифметике сложение, вычитание выполняется относительно некоторого фиксированного числа, которое называется модуль. Типичными значениями модулей, используемые в криптографии, являются 2, 10 и 26. Какой бы модуль мы ни взяли, все встречающиеся числа заменяются на остатки от деления этих чисел. Если в остатке получается отрицательное число, то к нему прибавляют значение модуля, чтобы остаток стал неотрицательным. Например, если используется модуль 26, то единственно возможные числа лежат в диапазоне от 0 до 25. Так, если прибавить 17 к 19, то результат равен 10, поскольку 17+19 = 36, а 36 при делении на 26 дает остаток 10. Чтобы указать, что используется модуль 26, принята форма записи:
17+19=10(mod26).
Если вычесть 19 из 17, то результат (-2) получается отрицательным, поэтому к нему прибавляется 26, и в итоге получается 24.
При сложении по модулю 26 двух числовых последовательностей сформулированные правила сложения применяются в каждой паре чисел по отдельности, без «переноса» на следующую пару. Аналогично, при вычитании по модулю 26 одной числовой последовательности из другой правила вычитания применяются к каждой паре чисел по отдельности, без «заимствования» из следующей пары.
Пример 1.1
Сложить по модулю 26 последовательности 15 11 23 06 11 и 17 04 14 19 23
и в результате 06 15 11 25 08
Если модуль равен 10, то используются числа от 0 до 9; при модуле 2 – только 0 и 1
Арифметика по модулю 2, или, как ее обычно называют, двоичная (бинарная) арифметика, имеет особое значение, поскольку в этом случае сложение и вычитание являются идентичными операциями, т.е всегда дают одинаковый результат, а именно:
0 1 0 1 - 0 1 0 1
0 1 1 2 0 -1 1 0
0 1 1 0 0 1 1 0 (mod 2) в обоих случаях.
Модульное сложение и вычитание букв
Давайте рассмотрим пример модульного сложения и вычитания применимо к буквам.
Прибавить TODAY к NEVER по модулю 26
Вычесть TODAY из NEVER по модулю 26
Решение
TODAY= 19 14 03 00 24
NEVER= 13 04 21 04 17
Сумма = 32 18 24 04 41 06 18 24 04 15 = GSYEP
TODAY= 19 14 03 00 24
NEVER= 13 04 21 04 17
Разность = 06 10 -18 -04 07 06 10 08 22 07 = GKIWH
Краткие итоги
В лекции рассмотрены вопросы, связанные с шифрование и дешифрованием текстов. Даны определения кода, шифра, дешифровки, криптографии. Рассмотрено применение модульной арифметики к вопросам шифрования.
Контрольные вопросы
Дайте определение монографа, диграфа, триграфа и полиграфа чем они отличаются друг от друга.
Дайте определение символа.
Дайте определение строки.
Как определяется длина строки?
Что такое система шифрования?
Дайте определение терминам зашифрование и расшифрования.
Чем расшифрование отличается от дешифрования?
Дайте определение криптографии, и кто ей занимается.
Назовите этапы дешифрования и охарактеризуйте их.
Дайте определение кода и шифра.
Как оценить стойкость шифра?
Дайте определение кодам, обнаруживающим и исправляющим ошибки.
Назовите методы сокрытия содержания сообщений.
Дайте определение модульной арифметике и ее предназначение для шифрования текстов.
Теоретико-числовая база построения системы остаточных классов
Напомним определение деления с остатком.
Определение
Говорят, что целое число делится на натуральное число с остатком, если имеется пара целых чисел и , таких, что и . называется делимым, - делителем, - неполным частным, - остатком.
Для целых чисел:
Определение
Говорят, что целое число делится на целое число с остатком, если имеется пара целых чисел и , таких, что и .
Пример :
48 при делении на 5 даёт остаток 3 , т.к. , , -48 при делении на 5 даёт остаток 2 , т.к. , .
Сравнения и их основные свойства
Возьмём произвольное фиксированное натуральное число и будем рассматривать остатки при делении на различных целых чисел.
При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.
Определение
Два целых числа и называются сравнимыми по модулю , если их разность делится без остатка на .
Символически сравнимость записывается в виде формулы (сравнения ):
Число называется модулем сравнения.
Эквивалентная формулировка:
Определение
Целые числа и называются сравнимыми по модулю , если остатки от деления этих чисел на равны.
Отношение сравнимости по модулю обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности.
Отнесём все целые числа, дающие при делении на один и тот же остаток в один класс, поэтому получится различных классов по модулю . Множество всех чисел сравнимых с по модулю называется классом вычетов по модулю .
Подробнее о свойствах сравнений и классах вычетов смотри Сравнения и их основные свойства
Теорема о делении с остатком. Алгоритм Евклида
Теорема о делении с остатком
Для любых целых и , , существует единственный набор целых чисел и , что и , где - модуль числа .
На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.
Алгоритм Евклида для целых чисел
Пусть и - целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое - это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
Тогда НОД , наибольший общий делитель и , равен , последнему ненулевому члену этой последовательности.
Существование таких , то есть возможность деления с остатком на для любого целого и целого , доказывается индукцией.
Корректность этого алгоритма вытекает из следующих двух утверждений:
Китайская теорема об остатках
Фундаментальным положением, лежащим в основе модулярного представления чисел, является китайская теорема об остатках (Chinese Remainder Theorem - CRT). Например, эта теорема гарантирует, что при правильном выборе модулей СОК каждое число из динамического диапазона имеет в СОК единственное представление, и по этому представлению можно определить представленное число. В своей первоначальной формулировке эта теорема была доказана китайским математиком Сунь-Цзы приблизительно в 100 г. н.э. В современной формулировке теорема звучит так:
Теорема
Пусть - попарно взаимно простые числа, большие 1, и пусть . Тогда существует единственное неотрицательное решение по модулю следующей системы сравнений:
, , , .Другими словами, отображение, которое каждому целому числу , , ставит в соответствие кортеж , где является биекцией кольца на декартово произведение колец .
Теоремы Эйлера и Ферма, их роль в вычислении мультипликативных обратных элементов по заданному модулю
Определение
Функция Эйлера - это количество чисел от до , взаимно простых с .
Т.е. это количество таких натуральных чисел из отрезка , наибольший общий делитель (НОД) которых с равен единице.
Tеоремa Эйлера
Если и взаимно просты, то , где - функция Эйлера.
Частным случаем теоремы Эйлера является малая теорема Ферма.
Малая теорема Ферма
Если - простое число и - произвольное целое число, не делящееся на , то .
Числа Мерсенна, Ферма и операции над ними
При рассмотрении отдельных классов простых чисел интерес представляет вопрос о простых числах специального вида, например, таких как числа Мерсенна или числа Ферма.
Определение
Числа Мерсенна
- числа вида ![]() , где - натуральное число.
Названы в честь французского математика Марена Мерсенна.
, где - натуральное число.
Названы в честь французского математика Марена Мерсенна.
Иногда числами Мерсенна называют только числа с нечетными или простыми индексами n .
Множества простых чисел в этих последовательностях совпадают, а потому понятие простого числа Мерсенна не зависит от того, как именно определяются числа Мерсенна.
При простых значениях n = p число может оказаться простым, но может быть составным. Например, при мы получаем простые числа Мерсенна: , а при числа - составные.
Определение
Числа Ферма
- числа вида ![]() , где n
- неотрицательное целое число.
, где n
- неотрицательное целое число.
При числа Ферма простые: . Известно, что для числа являются составными. На 2014 г. не найдено ни одного простого числа такого вида для .
Все числа Мерсенна и Ферма – взаимно простые. Кроме того, для модулей СОК вида ![]() ,
, ![]() легко реализуется преобразование и арифметические операции. Поэтому эффективно выбирать модули СОК в виде чисел Мерсенна и Ферма.
легко реализуется преобразование и арифметические операции. Поэтому эффективно выбирать модули СОК в виде чисел Мерсенна и Ферма.
Математические модели модулярного представления и параллельной обработки информации
Определение системы остаточных классов
Представление чисел в виде набора остатков от деления на выбранные натуральные модули - основания системы называется системой остаточных классов - СОК (residue number system - RNS) или модулярной системой счисления - МСС (modular system).
Выбор СОК как системы счисления
Под системой счисления понимают совокупность символический метод записи чисел, представление чисел с помощью письменных знаков, или, точнее, способ кодирования (представления) элементов некоторой конечной модели действительных чисел словами одного или более алфавитов.
К любой кодовой системе применимы следующие требования:
- возможность представления в данной системе любой величины в рассматриваемом, заранее назначенном диапазоне;
- единственность представления – любая кодовая комбинация соответствует одному и только одному числу в заданном диапазоне;
- простота оперирования числами в данной системе счисления.
Системы счисления подразделяются на позиционные, непозиционные и смешанные. (Система счисления)
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Обычно используется b-ричная система счисления, которая определяется целым числом b>1, называемым основанием системы счисления.
Смешанная система счисления является обобщением b-ричной системы счисления и также зачастую относится к позиционным системам счисления. Смотри Полиадический код .
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от её положения в числе. При этом система может накладывать ограничения на положение цифр.
Всякая вычислительная структура тесно связана с системой счисления, в которой она работает.
В обычной позиционной системе счисления (ПСС) значение разряда любого числа, кроме младшего, являющегося результатом двухместной арифметической операции, зависит не только от значения одноимённых операндов, но и от всех младших разрядов, т. е. ПСС обладает строго последовательной структурой. Напротив, непозиционные коды с параллельной структурой позволяют реализовать распараллеливание операций на уровне выполнения элементарных арифметических действий.
В качестве такой непозиционной системы удобна система остаточных классов (СОК).
Базовые арифметические операции в СОК делятся на две группы: модульные и немодульные.
- Модульные операции, которые могут быть выполнены параллельно и независимо над отдельными цифрами чисел: сложение, умножение, вычитание без знака.
- Немодульные операции, которые требуют знания величины модулярных чисел в целом: сравнение, вычитание с получением отрицательного результата, контроль переполнения модулярного числа.
Основным достоинством системы остаточных классов является сравнительная простота выполнения модульных операций, недостатком - большая трудоемкость немодульных операций.
Модульные операции над числами в системе остаточных классов
Возможность применения СОК в вычислительных алгоритмах обусловлено наличием определённого изоморфизма между математическими операциями над целыми числами и соответствующими операциями над системой целых неотрицательных остатков по отдельным модулям. Сложение, умножение, возведение в целую положительную степень любых целых положительных чисел идентичны соответствующим операциям, выполняемым над системой остатков.
Основные методы и алгоритмы перехода от позиционного представления к остаткам
Обычно исходные данные для вычислений представлены в каком-либо традиционном представлении, двоичном или десятичном. В таком же виде ожидаются результаты вычислений. Отсюда понятна необходимость перевода чисел из позиционного представления в представление СОК (прямое преобразование) и обратно (обратное преобразование). Одной из первых немодульных процедур является прямое преобразование позиционных кодов в код СОК.
Перевод числа в систему остаточных классов можно осуществить непосредственно методом деления, с модулями СОК в качестве делителей. Однако из-за сложности операции деления техническая реализация такого метода неэффективна. Поэтому рассматриваются другие методы. Например, часто используется метод перевода числа из позиционной системы счисления в СОК, не содержащий операции деления, называемый методом непосредственного суммирования модульных значений разрядов позиционного числа.
Восстановление позиционного представления числа по его остаткам
Система остаточных классов обладает одной особенностью, которую можно отнести к недостаткам этой системы: нельзя визуально определить величину числа, представленного в СОК, а следовательно затруднительно и выполнение таких операций, как сравнение чисел, определение знака числа. Один из путей решения этой проблемы состоит в преобразовании чисел из СОК в позиционную систему счисления. Оценим существующие способы перевода, как традиционные: метод ортогональных базисов; перевод числа в обобщенную позиционную систему (ОПС), так и недавно появившиеся интервальные методы перевода.
Метод ортогональных базисов
Метод восстановления числа по его остаткам был найден еще в Китае две тысячи лет назад. Основой этого метода является теорема, названная Китайской теоремой об остатках (КТО) .
Эта теорема лежит в основе метода ортогональных базисов при переводе из системы остаточных классов в позиционную систему счисления.
Перевод числа из СОК в обобщенную позиционную систему (ОПС)
Еще один метод определения величины числа связан с переводом числа из системы остаточных классов в ОПС. Для того, чтобы рассмотреть этот метод, выявим связь между представлением некоторого числа в этих двух системах.
Пусть по-прежнему СОК задается основаниями и - число в этой системе. И пусть являются также основаниями ОПС, тогда число можно представить в виде
где – коэффициенты (цифры) ОПС.
Очевидно, что диапазоны чисел, представимых в СОК и ОПС совпадают, т.е. можно говорить о наличии взаимно однозначного соответствия между множеством представлений чисел в СОК и ОПС.
Это равенство можно переписать в следующем виде:
,откуда следует, что цифры ОПС могут быть получены из соотношений:
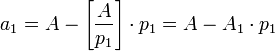 , где ,
, где ,
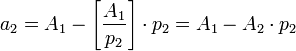 , где ,
, где
, где ,
, где 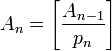 .
.
Причем при определении цифр по этим формулам все вычисления можно вести в СОК.
Интервальные методы перевода
Достаточно эффективными методами перевода чисел из СОК в ПСС являются интервальные методы, основанные на интервальных характеристиках чисел. Одна из таких характеристик – номер интервала.
Расширение диапазона представления чисел
Расширение системы оснований является одной из основных немодульных операций в СОК. Выполнение этой операции бывает необходимо при выполнении операции деления чисел, при вычислении позиционных характеристик, при обнаружении переполнения при выполнении сложения или умножения чисел.
Задачу расширения системы оснований можно сформулировать следующим образом: найти остаточное представление числа по новому основанию (новым основаниям), если известно представление числа по другим основаниям (остатки от деления на другие числа). Один из путей расширения системы оснований состоит в переводе числа в позиционную систему счисления и вычисления остатка от деления на новый модуль. Этот путь не является рациональным с точки зрения числа операций.
Другой метод расширения системы оснований позволяет определить цифру числа по новому основанию, базируясь на таких позиционных характеристиках числа, как ранг числа, след числа.
Литература
Бухштаб А. А. Теория чисел – М: Наука, 1975 г.
Айерленд К. Классическое введение в современную теорию чисел. М: Мир, 1987.
Акушинский И. Л., Юдицкий Д. И. Машинная арифметика в остаточных классах. – М. Советское радио, 1968.
Амербаев В. М. Теоретические основы мащинной арифметики, - Алма –Ата: Наука, 1976.
Дополнительно :
Сизый С. В. Лекции по теории чисел. Учебное пособие для математических специальностей. Екатеринбург, Уральский государственный университет им. А.М.Горького, 1999.
Транскрипт
1 МОДУЛЬНАЯ АРИФМЕТИКА В некоторых приложениях удобно выполнять арифметические операции над целыми числами, заданными в так называемом модульном представлении Это представление предполагает, что целое число представлено вычетами (остатками) по модулям из множества попарно взаимно простых чисел Вычет числа по модулю m обозначают mod m Например, mod 5 ; 8 mod mod В этом разделе под размерностью задачи мы будем понимать не количество чисел на входе алгоритма, как например, в задаче сортировки, а количество битов, использованных для записи числа Алгоритм, получающий на вход целые числа, называется полиномиальным, если его время работы ограничено многочленом от log, log, log, те многочленом от длин исходных данных (в двоичной системе счисления) Если, это попарно взаимно простых чисел и, то любое целое число u, такое что u, можно однозначно представить множеством его вычетов u, u, u, где u u mod, Обычно пишут u (u, u, u) Сложение, вычитание и умножение легко выполняются, если их результаты заключены между и, те если их можно рассматривать как вычисления по модулю Пусть два целых числа u и v заданы их множествами вычетов, те u (u, u, u) и v (v, v, v) Тогда операции сложения, умножения и вычитания определяются следующим образом: u + v (w, w, w), где w (u + v) mod ; () u v (,), где (u v) mod ; () uv (y, y, y), где y uv mod () Рассмотрим пример Пусть, 5, 7 Получаем Тогда 6 (,6), так как 6 mod, 6 mod5, 6 mod 7 6 Аналогично, 9 (,), 5 (,) В силу () (,), так как (+) mod, (+) mod5, (6 +) mod 7 но нетрудно убедиться, что 5 (,) Согласно () и () получаем: 6 9 (,) это модульное представление числа 6 9 (,5) это модульное представление числа 5 Операция деления в модульной арифметике не определена Преимущество модульного представления состоит в том, что арифметические операции могут быть реализованы с меньшими вычислительными затратами, чем при обычном представлении, так как вычисления выполняются независимо для каждого модуля Следующая теорема доказывает, что соответствие u (u, u, u) является взаимно однозначным КИТАЙСКАЯ ТЕОРЕМА ОБ ОСТАТКАХ Пусть, попарно взаимно простые целые числа, и u u mod Тогда соответствие u (u, u, u) между целыми числами u в
2 интервале [,) и наборами вида (u, u, u), u < при <, взаимно однозначно Доказательство Очевидно, что для каждого числа u найдется соответствующий членный набор, так как в интервале [,) заключено ровно значений переменной u и допустимых членных наборов также ровно, так как Достаточно показать, что каждый набор соответствует не более, чем одному числу u Допустим, что два числа u и v, u < v <, соответствуют набору (u, u, u) Тогда разность u v должна делиться на каждое из чисел, так как все взаимно простые, то разность u v должна делиться и на Но u v и u v делится на, те u и v должны отличаться не менее, чем на, а значит не могут оба принадлежать интервалу [,) Результаты аналогичные результатам для целых чисел, справедливы и для полиномов Пусть), () это попарно взаимно простые полиномы, (Тогда любой полином u () такой, что deg(u) < deg(()) можно однозначно представить последовательностью u, u, u ()) остатков от деления (u () на каждый полином () Полином u () это тот единственный полином, для которого deg(u) < deg() и u q + u для некоторого полинома q () Мы в этом случае будем использовать обозначение u u() mod аналогично модульной записи целых чисел По аналогии с целыми числами можно показать, что соответствие u () (u, u(), u ()) взаимно однозначное Пример Пусть, + +, + 5 Рассмотрим u Получаем u mod 6, u mod, u mod +, u mod, таким образом, u (6, +,) Для того, чтобы можно было пользоваться модульной арифметикой, нужны алгоритмы, осуществляющие переход от позиционного представления к модульному и обратно Один из методов перехода от позиционного представления к модульному состоит в том, чтобы разделить число u на каждый из модулей, < Допустим, что каждое из чисел представлении Тогда произведение модулей содержит b разрядов в двоичном требует порядка b двоичных разрядов для записи двоичного представления, а деление u на каждое из чисел, где u <, могло бы потребовать делений b -битового числа на b -битовое число Разбив каждое деление на делений b -битовых чисел на b - битовые, можно перейти к модульному представлению за время O (D(b)), где D (n)
3 время деления n -разрядного двоичного целого числа на n -разрядное, как показано в А Ахо, Дж Хопкрафт, Дж Ульман Построение и анализ вычислительных алгоритмов D (n) O(n log n log log n) Модульное представление числа можно вычислить гораздо быстрее, если использовать следующий метод Очевидно, что, если нужно найти вычеты, например числа 8 по модулям, 5, 7, то можно сначала найти 8 mod5 5 и 8 mod 77, а затем 5 mod, 5 mod5, mod 7 и mod вместо вычисления 8 mod, 8 mod5, 8 mod 7 и 8 mod Вместо того, чтобы делить число u на каждый из модулей, сначала вычисляем произведения модулей:, затем, 5 6 7, и тд Далее вычисляем вычеты u и u числа u по модулям / и / / +, соответственно Теперь задача вычисления u mod, сведена к двум задачам половинного размера, а именно, u mod u mod для < /, и u mod u mod для / < Далее вычисляем вычеты u и u числа u по модулям / и / / + / и вычеты u, u числа u по модулям / / + / и / / + Таким образом, в свою очередь каждая из подзадач может быть сведена к двум задачам половинного размера, а именно, u mod u mod для < /, и u mod u mod для / < /, u mod u mod для / < / и u mod u mod для / < Время выполнения этого алгоритма можно оценить следующим образом: D (b /) + D(b /) + + D(b) (b/)log (b/)log log (b/) + (b/)log (b/)log log (b/) (b)log blog log b (blog log (b) b(log) /)log log (b) blog log b Выигрыш по времени по сравнению с делением на каждый модуль приблизительно равен blog b blog log b log Блок-схема быстрого алгоритма нахождения модульного представления числа приведена на Рис Вход: Модули (I), I, и целое число u, выход: вычеты t M (I), I, целого числа u по модулям (I) Заметим, что Пример работы алгоритма Пусть, те t Заданы модули, Вычисляем произведения модулей и запоминаем их в массиве q Индекс I номер произведения, индекс J номер шага q q q q q q q q q q u mod q u mod q
if ($this->show_pages_images && $page_num doc["images_node_id"]) { continue; } // $snip = Library::get_smart_snippet($text, DocShare_Docs::CHARS_LIMIT_PAGE_IMAGE_TITLE); $snips = Library::get_text_chunks($text, 4); ?>4 q u mod mod mod q mod q mod q mod q q M M M M
5 I: q (I,) (I) J: t I: : J q(I, J) q(I, J) * q(I + J, J) (, t) u J t: : I: : J (I, J) (I, J) mod q(I, J) (I + J, J) (I, J) mod q(I, J) I: M (I) (I,) Рис Быстрый алгоритм нахождения модульного представления числа
6 ПРИМЕНЕНИЕ КИТАЙСКОЙ ТЕОРЕМЫ ОБ ОСТАТКАХ Рассмотрим задачу преобразования модульного представления целого числа в его позиционное представление Процесс восстановления числа по его остаткам был известен китайцам более лет назад, и потому соответствующую теорему называют китайской теоремой об остатках Пусть даны попарно взаимно простые модули, и вычеты u, u, u, где u u, u, u) Пусть (Лемма Пусть c произведение всех d t, надо найти такое целое число u, что, кроме, те c mod, те d c mod и d < Тогда Число c делится на при Так как c d mod u c d u mod, где c / Доказательство, так что c d u mod, Следовательно, то c d u c d u c d u u mod mod Так как делит, то эти соотношения выполняются и тогда, когда все арифметические операции производятся по модулю Таким образом, Лемма доказана Пример Пусть, 5, 7, 5 и модульное представление числа имеет вид (,) Восстановим число по его модульному представлению Для этого вычислим c 5, c и c 5 Нетрудно проверить, что d так как 5 mod, d так как mod5 и d, 5 mod 7 Тогда по теореме получаем u c d u mod mod 59 Задача состоит в эффективном вычислении c du mod В рассмотренном примере d мы вычисляли перебором Ниже будет показано, как это можно сделать непереборным методом НАИБОЛЬШИЕ ОБЩИЕ ДЕЛИТЕЛИ И АЛГОРИТМ ЕВКЛИДА Пусть и положительные целые числа Положительное целое число g называется наибольшим общим делителем чисел и, обозначается HOD (,), если: g делит и, Всякий общий делитель и делит g Можно показать, что для положительных целых и такое число g единственно Например, HOD (57,)
7 Алгоритм Евклида для вычисления HOD (,) состоит в вычислении последовательности остатков, где, представляет собой ненулевой остаток от деления на и нацело делит, те + Тогда HOD (,) Другими словами этот алгоритм вычисляет + q для <, где q / Рассмотрим пример Пусть 57, а, следовательно HOD (57,) Блок-схема алгоритма Евклида приведена на Рис ТЕОРЕМА Алгоритм Евклида правильно находит значение HOD,) (Доказательство Алгоритм вычисляет + q для < q / Так как + < при, то алгоритм сходится, те заканчивает работу Из формулы + q следует, что HOD(,) делит +, но так как + + q, то HOD (+,) делит Таким образом, получаем, что HOD (,) HOD (,) HOD(,) Алгоритм Евклида можно расширить так, чтобы он находил не только HOD (,), но и целые числа и y, такие, что + y HOD(,) Блок-схема расширенного алгоритма Евклида показана на Рис, где
8 A, A Q A / A A A Q A A? Да Нет Печать A AA AA Рис Алгоритм Евклида
9 A, A, / A A Q A Q A A A? Печать A, Да A A A A Q Q Рис Расширенный алгоритм Евклида
10 Пример Для 57 и получаем q 57 q y y yq 9 y () 9 6 () y y 5 (5) Таким образом, HOD (57,) 57 () + 7 ЛЕММА В расширенном алгоритме Евклида + y при () Доказательство При +, При + Пусть равенство () справедливо для и Покажем, что () справедливо для + В соответствии с расширенным алгоритмом Евклида + q, y + y qy Отсюда следует, что + + y+ + y q(+ y) (5) По предположению + + y+ q, но в соответствии с алгоритмом Евклида q +, те имеем + + y+ +, лемма доказана Выше при рассмотрении вопроса о восстановлении числа по его модульному представлению мы находили числа d c mod, До сих пор мы делали это перебором Рассмотрим, как расширенный алгоритм Евклида может быть применен для нахождения числа обратного к данному по некоторому модулю Уравнение вида b mod, где, b и целые числа называют линейным диофантовым уравнением Очевидно, что в нашем случае это уравнение имеет вид mod (6) Известно, что в этом частном случае, если HOD (,), то уравнение имеет единственное решение, и это решение представляет собой элемент обратный к по модулю n Уравнение (6) можно переписать в виде + y, (7) где y некоторое целое число
11 Нетрудно видеть, что если HOD (,), то (7) представляет собой разложение HOD (,), которое может быть найдено с помощью расширенного алгоритма Евклида Таким образом, элемент обратный к по модулю может быть найден с помощью расширенного алгоритма Евклида Пример Пусть, 5, 7, 5 и модульное представление числа имеет вид (,) Восстановим число по его модульному представлению Для этого вычислим c 5, c и c 5 Обратные к c элемент d найдем с помощью расширенного алгоритма Евклида Положим c и (примечание: всегда должно выполняться >) 5 y y () Отсюда получаем 5 () +, а искомое d mod Аналогично находим, d и d Окончательно получаем, u c d u mod mod 5 6
ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа). II 1 / 78 Часть I Конечные поля (поля Галуа). II ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа). II 2 / 78 Поля вычетов по модулю простого
6. Быстрые алгоритмы деления Деление чисел методом Ньютона Для определенности будем считать, что делимое a = (a, am) и делитель b = (b, b) записаны в позиционной системе счисления по основанию ().
ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля или поля Галуа. II 1 / 78 Часть I Конечные поля или поля Галуа. II ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля или поля Галуа. II 2 / 78 Поля вычетов по модулю
ЛЕКЦИЯ 6 СТЕПЕННЫЕ ВЫЧЕТЫ Пусть дан модуль n и некоторое число a, взаимно простое с модулем n. Рассмотрим последовательность степеней a, a 2, a t, Найдем наименьшее число k, при котором a k 1 mod n. Определение.
4 Теория чисел 4 Целые числа 7 Определение Пусть, b Z Тогда делит b, если существует целое число такое что b (обозначается b) 73 Теорема (деление с остатком) Если, b Z и b, тогда найдутся такие целые
ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа). I 1 / 67 Часть I Конечные поля (поля Галуа). I ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа). I 2 / 67 Поля вычетов по модулю простого
Http://vk.ucoz.et/ Операции над многочленами k a k Многочленом (полиномом) степени k называется функция вида a, где переменная, a - числовые коэффициенты (=,.k), и. Любое ненулевое число можно рассматривать
Лекция 4. СТАНДАРТ AES. АЛГОРИТМ RIJNDAEL. Стандарт AES (Advnced Encrypton Stndrd) представляет собой новый стандарт шифрования с одним ключом, который заменил стандарт DES. Алгоритм Rjndel (рейн-дал)
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ, каф Информационных Систем ВДКОЛЕСНИК УЧЕБНОЕ ПОСОБИЕ ПО КУРСУ «КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ СООБЩЕНИЙ (Алгебраическая теория блоковых кодов)»
ЛЕКЦИЯ 3 ВЫЧИСЛЕНИЕ КВАДРАТНЫХ КОРНЕЙ ПО МОДУЛЮ Случай простого модуля Рассмотрим сравнение х a mod р, () где число р простое и целое число а не делится на p Вычисление решения x данного уравнения является
Югорский физико-математический лицей ВП Чуваков ОСНОВЫ ТЕОРИИ ЧИСЕЛ Конспект лекций (0)(mod) (0)(mod) Натуральные числа N, - множество натуральных чисел, используемых для счета или перечисления
ЛЕКЦИЯ 3 ОТНОШЕНИЕ СРАВНИМОСТИ Возьмем натуральное целое число m, которое будем называть модулем. Определение. Целые числа a и b называются сравнимыми по модулю m, если разность (a b) делится на m (m a
Дополнительный материал Степенные вычеты Пусть дан модуль n и некоторое число, взаимно простое с модулем n Рассмотрим последовательность степеней, 2, t, Найдем наименьшее число k, при котором k mod n
Тема. Основы элементарной теории чисел и приложения- Теоретический материал. Множество вычетов по модулю, свойства сравнений. Пусть натуральное число, большее. Через Z обозначаем множество всех классов
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Понятие многочлена Определения Многочленом от одной переменной называется выражение вида
ЛЕКЦИЯ 1 НЕКОТОРЫЕ ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЕЛ В пособии не излагается теория чисел а дан минимальный инструментарий из этой теории который в дальнейшем потребуется для изучения криптографических систем используемых
УДК 68. Н.И. Червяков, И.Н. Лавриненко, С.В. Лавриненко, О.С. Мезенцева МЕТОДЫ И АЛГОРИТМЫ ОКРУГЛЕНИЯ, МАСШТАБИРОВАНИЯ И ДЕЛЕНИЯ ЧИСЕЛ В МОДУЛЯРНОЙ АРИФМЕТИКЕ (Ставропольский военный институт связи ракетных
ПРОЕКТНАЯ РАБОТА ПО МАТЕМАТИКЕ ЦИКЛЫ В РЯДУ ОСТАТКОВ ОТ ДЕЛЕНИЯ ЧИСЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ ФИБОНАЧЧИ Ученица: Безменова Саша Класс: 8 Руководитель: Сгибнев А. И. Последовательность Фибоначчи это последовательность,
Арифметические алгоритмы Простые числа Решето Эратосфена Поиск делителей (наименьший и наибольший) Разложение числа на множители НОД и НОК Перевод в другую систему счисления Арифметика остатков Простые
ЛЕКЦИЯ 7 ПЕРВООБРАЗНЫЕ КОРНИ Определение. Класс [a], где (a, n) = 1, называется первообразным корнем по модулю n, если показатель числа a по модулю n равен φ(n) значению функции Эйлера для модуля n. Известно,
Разбор контрольной работы Общие комментарии по результатам проверки контрольной: 1 В вычислениях присутствует большое количество арифметических ошибок Само по себе возникновение арифметических ошибок неизбежно
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Многочлены Новосибирск Многочлены Рациональными
Лекция 7 Комплексные числа их изображение на плоскости Алгебраические операции над комплексными числами Комплексное сопряжение Модуль и аргумент комплексного числа Алгебраическая и тригонометрическая формы
Системы счисления Система счисления способ записи чисел с помощью заданного набора специальных символов (цифр). В вычислительной технике применяются позиционные системы счисления, в которых значение цифры
Лекция 2 Тема: Сложение и вычитание векторов Умножение вектора на число НДУ коллинеарности План лекции Сложение векторов 2 Вычитание векторов Модуль суммы и модуль разности векторов 3 Определение и свойства
Тождественные преобразования алгебраических выражений Алгебраические выражения выражения, содержащие числа и буквы, связанные алгебраическими действиями: сложением, вычитанием, умножением, делением и возведением
Решение задач по теории чисел 1 Сравнения первой степени с одним неизвестным ax b (mod m) Пример 1. Решите сравнение О.В. Митина 1287x 447 (mod 516). (1) Решение: 1) Заменим коэффициенты сравнения (1)
Глава Целые числа Теория делимости Целыми называются числа, -3, -, -, 0, 3, те натуральные числа, 3, 4, а также нуль и отрицательные числа -, -, -3, -4, Множество всех целых чисел обозначается через
Указания, решения, ответы УРАВНЕНИЯ В ЦЕЛЫХ ЧИСЛАХ. Уравнение с одной неизвестной.. Решение. Подставим в уравнение. Получим равенство (4a b 4) (a b 8) 0. Равенство A B 0, где А и В целые, выполняется,
ЛЕКЦИЯ 2 ВЫЧИСЛЕНИЕ НАИБОЛЬШЕГО ОБЩЕГО ДЕЛИТЕЛЯ Алгоритм Евклида При работе с большими составными числами их разложение на простые множители, как правило, неизвестно. Но для многих прикладных задач теории
Глава 2 Целые, рациональные и вещественные числа 2.. Целые числа Числа, 2, 3,... называются натуральными. Множество всех натуральных чисел обозначается N, т.е. N = {,2,3,...}. Числа..., 3, 2,0,2,3,...
Приложение 1 ГРУППЫ, КОЛЬЦА, ПОЛЯ Для криптографии алгебра является одним из основных инструментов в теоретических исследованиях и практических построениях криптографических преобразований Поэтому в этом
Лекция 2 Цифровые методы представления информации. Цифровые коды. Двоичная и шестнадцатиричная системы счисления. Перевод чисел из одной системы счисления в другую. Двоичная арифметика. Формы представления
Www.cryptolymp.ru XIX Межрегиональная олимпиада школьников по математике и криптографии (11 класс) Решение задачи 1 Сначала заметим, что если N pq, где p и q простые числа, то количество натуральных чисел,
Алгебраические многочлены. 1 Алгебраические многочлены степени n над полем K Определение 1.1 Многочленом степени n, n N {0}, от переменной z над числовым полем K называется выражение вида: fz = a n z n
1 КОМПЛЕКСНЫЕ ЧИСЛА Комплексные числа в алгебраической форме 1Основные понятия Определение 1 Комплексным числом в алгебраической форме называется выражение вида, где и действительные числа, а так называемая
ЛЕКЦИЯ 12 СРВНЕНИЯ ВТОРОЙ СТЕПЕНИ ПО ПРОСТОМУ МОДУЛЮ И КВАДРАТИЧНЫЕ ВЫЧЕТЫ Общий вид сравнения второй степени по простому модулю р имеет вид (1) с 0 х 2 + с 1 х + с 2 0 mod p. Поиск решения сравнения (1)
XIX Межрегиональная олимпиада школьников по математике и криптографии Задачи для 11 класса Решение задачи 1 Сначала заметим, что если N = pq, где p и q простые числа, то количество натуральных чисел, меньших
ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля или поля Галуа. I 1 / 71 Часть I Конечные поля или поля Галуа. I ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля или поля Галуа. I 2 / 71 Поля вычетов по модулю простого
Решение нелинейных уравнений Не всегда алгебраические или трансцендентные уравнения могут быть решены точно Понятие точности решения подразумевает:) возможность написания «точной формулы», а точнее говоря
20. Неприводимые многочлены над основными числовыми полями Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Основная теорема алгебры В
Лекция. КОМПЛЕКСНЫЕ ЧИСЛА.. Числовое поле. Числовое поле множество чисел, в котором корректны арифметические операции: сложение, вычитание, умножение, деление на ненулевое число. Примеры числовых полей:
ЛЕКЦИЯ 16 КОНЕЧНЫЕ ПОЛЯ АЛГЕБРЫ И АЛГЕБРЫ С ДЕЛЕНИЕМ АЛГЕБРА КВАТЕРНИОНОВ ТЕОРЕМА ФРОБЕНИУСА 1 КОНЕЧНЫЕ ПОЛЯ Лемма 1. Если поле F состоит из q элементов, то каждый элемент поля F является корнем многочлена
5 Конечные поля 5.1 Конечные поля Определение 5.1. Кольцом R, +, называется множество R с двумя бинарными операциями + и такими, что 1) R, + абелева группа; 2) операция ассоциативна, т. е. (a b) c = a
СИСТЕМА ЗАЩИТЫ ИНФОРМАЦИИ С ИСПОЛЬЗОВАНИЕМ МОДУ- ЛЯРНОЙ СИСТЕМЫ СЧИСЛЕНИЯ Калмыков И.А., Науменко Д.О., Березкина М.В., Макарова А.В., Калмыков М.И. Северо-Кавказский федеральный университет. Институт
Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0, коэффициентами
Г л а в а 3 КОЛЬЦА МНОГОЧЛЕНОВ 18. Многочлены от одной переменной 18.1. Определения и основные свойства. Многочленом от одной переменной над кольцом K называется выражение f = f(x) = a 0 + a 1 x +... +
Оглавление Краткие теоретические сведения... 3 Двоичная система счисления... 5 Восьмеричная и шестнадцатеричная системы счисления... 5 Перевод числа из одной позиционной системы счисления в другую... 6
Лабораторная работа 8 Вычисление наибольшего общего делителя для двух чисел при помощи алгоритма Евклида Цель работы используя алгоритм Эвклида создать программу, которая для чисел a и b определяет наибольший
Из истории математики Первой достаточно объемной книгой, в которой арифметика излагалась независимо от геометрии, было Введение в арифметику Никомаха (ок нэ) В истории арифметики её роль сравнима с ролью
ФГОБУ ВПО "СибГУТИ" Кафедра вычислительных систем Дисциплины "ЯЗЫКИ ПРОГРАММИРОВАНИЯ" "ПРОГРАММИРОВАНИЕ" Практическое занятие Работа с десятичными разрядами Преподаватель: Доцент Кафедры ВС, к.т.н. Поляков
Прикладная алгебра 1 / 160 Прикладная алгебра Лекции для групп 320 328 (III поток) 5-й семестр 2013/2014 уч. года Лектор Гуров Сергей Исаевич Ассистент Кропотов Дмитрий Александрович Факультет Вычислительной
Решение уравнений в целых числах Линейные уравнения. Метод прямого перебора Пример. В клетке сидят кролики и фазаны. Всего у них 8 ног. Узнать сколько в клетке тех и других. Укажите все решения. Решение.
2008 г 3 Труды ФОРА ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПРОСТЫХ И СОСТАВНЫХ ЧИСЕЛ Кубанский государственный университет, г. Краснодар Работа посвящена доказательству малой теоремы Ферма. В ней предлагается простой
ЛЕКЦИЯ 2. Алгоритмы циклической структуры. Цель лекции: Знакомство с понятием алгоритма циклической струк туры. Приобретение навыков построения алгоритмов циклической с трук т уры. 5. Алгоритмы циклической
Math-Net.Ru Общероссийский математический портал Е. П. Мачикина, Б. Я. Рябко, Быстрый метод перевода цепных дробей в обыкновенные, Дискрет. матем., 1999, том 11, выпуск 4, 152 156 DOI: http://dx.doi.org/10.4213/dm402
Co Компьютерная алгебра 9. Решение систем линейных алгебраических уравнений над кольцом целых чисел 9.1. Варианты метода Гаусса над полем рациональных чисел и над кольцом целых чисел Одним из самых широко
РЕШЕНИЕ РЕКУРРЕНТНЫХ УРАВНЕНИЙ Обозначим через значение некоторого выражения при подстановке в него целого числа Тогда зависимость члена последовательности от членов последовательности F F со значениями
Югорский физико-математический лицей ВП Чуваков Задача С6 (Теория чисел на ЕГЭ) Учебно-методическое пособие Ханты-Мансийск 0 ВП Чуваков Задача С6 (Теория чисел на ЕГЭ): Учебнометодическое пособие, - Ханты-Мансийск,
2.22. Вынесите за скобки общий множитель (n натуральное число): 1) x n + 3 + x n ; 3) z 3n - z n ; 2) y n + 2 - y n - 2, n > 2; 4) 5 n + 4 + 2 5 n + 2-3 5 n + 1. 2.23. Каждому числу поставили в соответствие
Лекция 4 РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ЗАДАЧА О ЧИСЛЕ СЧАСТЛИВЫХ БИЛЕТОВ Рассмотрим следующую задачу Имеются билеты с номерами от 000000 до 999999 Счастливым признается билет, у которого сумма первых трех цифр
Тема 1-8: Комплексные числа А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков (1 семестр)
Тема 1-9: Многочлены. Построение кольца многочленов. Теория делимости. Производная А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной
Лекция: Неприводимые и приводимые многочлены. Теорема о построении полей из p n элементов, где p простое число, n 2. Вычисления в конечных полях, алгоритм Евклида. Расширения полей. Мультипликативная группа
Теория Галуа, лекция 2: расширения полей Миша Вербицкий 25 января, 2013 матфак ВШЭ 1 Расширения полей ОПРЕДЕЛЕНИЕ: Расширение поля k есть поле K, содержащее k. Отношение «быть расширением» обозначается
Стр. 1 из 18 Двоичная арифметика Числа которыми мы привыкли пользоваться называются десятичными и арифметика которой мы пользуемся также называется десятичной. Это потому, что каждое число можно составить
Оглавление Введение. Основные понятия.... 4 1. Интегральные уравнения Вольтерры... 5 Варианты домашних заданий.... 8 2. Резольвента интегрального уравнения Вольтерры. 10 Варианты домашних заданий.... 11


 Общероссийский народный фронт: как вступить в организацию?
Общероссийский народный фронт: как вступить в организацию? Сеголен Руаяль: фото, биография, личная жизнь, дети
Сеголен Руаяль: фото, биография, личная жизнь, дети Настоящая француженка кристин лагард Кристин лагард биография семья
Настоящая француженка кристин лагард Кристин лагард биография семья Но не из-за нелепых слов в эфире
Но не из-за нелепых слов в эфире